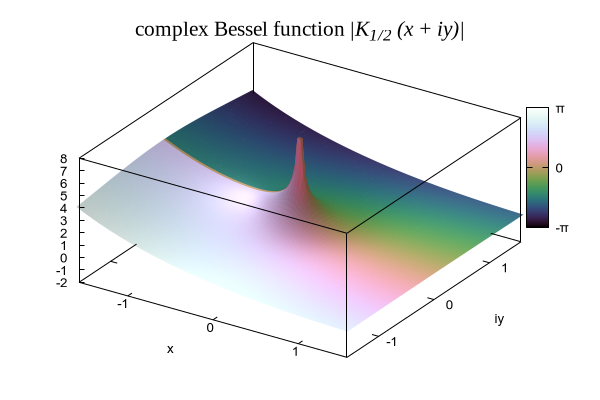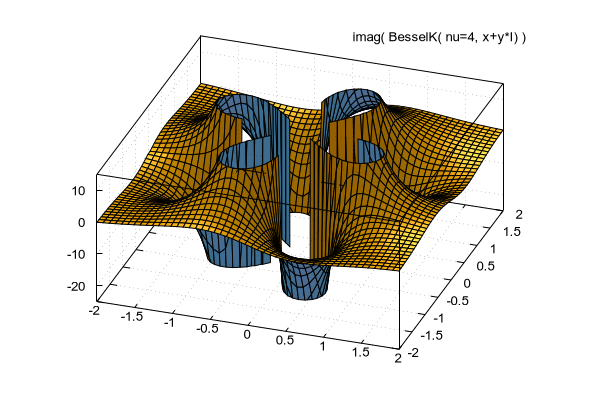
#
#
#
# Check support for BesselK
if (!strstrt(GPVAL_COMPILE_OPTIONS, "+AMOS")) {
print "This copy of gnuplot does not support BesselK"
exit # return to caller
}
save_encoding = GPVAL_ENCODING
set encoding utf8
set xrange [0:5]
set yrange [0:10]
set sample 201
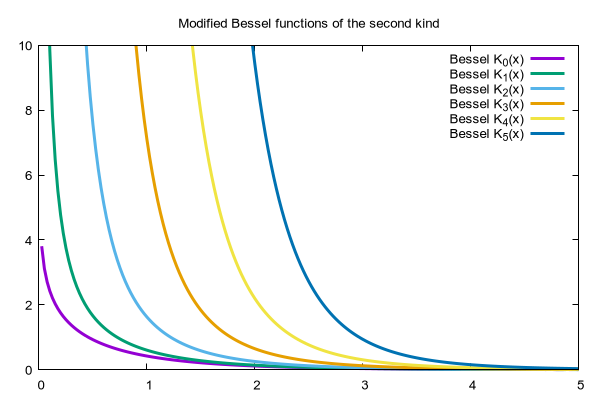
set title "Modified Bessel functions of the second kind"
plot for [K=0:5] BesselK(K,x) lw 3 title sprintf("Bessel K_{%d}(x)",K)
Click here for minimal script to generate this plot