#
# Set up a color mapping for vectors in the complex plane similar to the one
# used on Wikipedia for plotting complex trigonometric functions.
# HSV colors
# Hue is the vector angle atan( Real(f) / Imaginary(f) )
# Saturation is the vector magnitude (length)
# V = 1
#
save_encoding = GPVAL_ENCODING
set encoding utf8
# We don't use the palette for plotting, but defining it allows us to
# draw a colorbar showing the phase angle color scheme
set palette model HSV defined ( 0 0 1 1, 1 1 1 1 )
set cbrange [-pi : pi]
set cbtics ("0" -pi, "2π" pi)
set cblabel "Phase Angle" rotate offset -2,0
Hue(x,y) = (pi + atan2(-y,-x)) / (2*pi)
phase(x,y) = hsv2rgb( Hue(x,y), sqrt(x**2+y**2), 1. )
set xrange [-pi/2. : pi/2.]
set yrange [-pi/2. : pi/2.]
set urange [-pi/2. : pi/2.]
set vrange [-pi/2. : pi/2.]
set xtics ("-π/2" -pi/2., "-π/4" -pi/4., "0" 0, "π/4" pi/4., "π/2" pi/2.)
set ytics ("-π/2" -pi/2., "-π/4" -pi/4., "0" 0, "π/4" pi/4., "π/2" pi/2.)
set view map; set size square; unset key
set isosamples 100,100
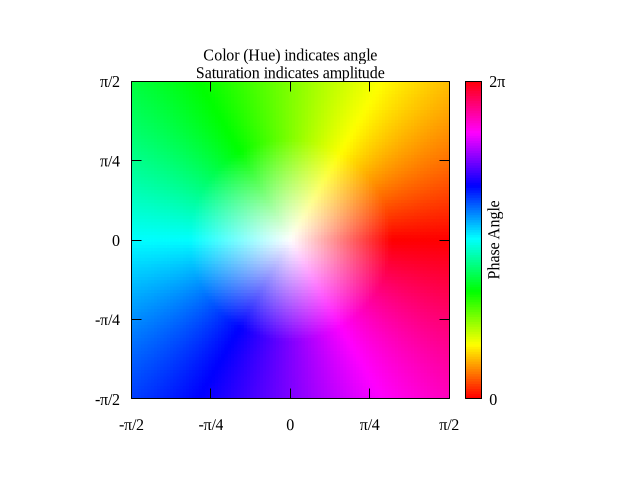
set title "Color (Hue) indicates angle\nSaturation indicates amplitude"
splot '++' using 1:2:(phase($1,$2)) with pm3d lc rgb variable
Click here for minimal script to generate this plot